Logarithm quantative aptitude question and answers
Logarithms have a wide range of applications in solving problems which are based not only on logarithms but also on the problems like finding the bigger number of 2^51 and 5^30. Logarithms also have many other applications which when used gives an immense sense of its usage.
What is a Logarithm?
A Logarithm is a quantity which represents the rise of it in terms of another number (base)
How it was derived, is there any formula to get logarithmic values?
Yes, there is a series called logarithmic series which will generate value of the logarithms
The main terms which one should be more familiar with before solving logarithmic problems are
Exponent: Power of a number.
Base: The number to reduce another number when log is applied.
Some Basic Logarithmic formula:
log ab = log a + log b
log a/b = log a - log b
log(a^b) = b*log(a)
logab = 1/logba
logbn = logen/logeb
log10n = logen/loge10 = logen *(0.43429448..)
Tool to find logarithm value of a number
*********************************************************************************
Solved problems:
Question 1: What is the value of STEP [ log25 ]?
Solution:
log25 = log105 / log102
= 0.6989/0.3010 { 2 < val < 3 }
STEP[log25 ] = 2
Question 2: Which is the bigger one 2^51 or 5^31 ?
Solution: Apply Log10 both sides
Log10(2^51) , Log10(5^31)
51*Log102 , 31*Log105
51*(0.3010) , 31*0.6989
15.3 , 21.7 (Approximately)
so 5^31 is the bigger one.
Exercise problems:
Print this page or save as pdf?
 |
| Logarithms |
A Logarithm is a quantity which represents the rise of it in terms of another number (base)
How it was derived, is there any formula to get logarithmic values?
Yes, there is a series called logarithmic series which will generate value of the logarithms
The main terms which one should be more familiar with before solving logarithmic problems are
Exponent: Power of a number.
Base: The number to reduce another number when log is applied.
Some Basic Logarithmic formula:
log ab = log a + log b
log a/b = log a - log b
log(a^b) = b*log(a)
logab = 1/logba
logbn = logen/logeb
log10n = logen/loge10 = logen *(0.43429448..)
Tool to find logarithm value of a number
*********************************************************************************
Solved problems:
Question 1: What is the value of STEP [ log25 ]?
Solution:
log25 = log105 / log102
= 0.6989/0.3010 { 2 < val < 3 }
STEP[log25 ] = 2
Question 2: Which is the bigger one 2^51 or 5^31 ?
Solution: Apply Log10 both sides
Log10(2^51) , Log10(5^31)
51*Log102 , 31*Log105
51*(0.3010) , 31*0.6989
15.3 , 21.7 (Approximately)
so 5^31 is the bigger one.
Exercise problems:
- What is the value of 1/Log26 + 1/Log36 + log61
- What is the value of Log26
- Which is the bigger one 5^81 or 8^40 ?
- Which is smaller 1/(5^81) or 1/(125^3) ?
- What is the value of Log160006
- What is the value of Log 1
- What is the value of Log( -10 )
- Loge6 v/s Log106 which is bigger one
Hope you have enjoyed the article, Support us :)
Let us know how many problems you have solved which helps others to correct their answers.
Have more interesting questions? comment and let us know.
For any queries feel free to drop a comment.
Print this page or save as pdf?
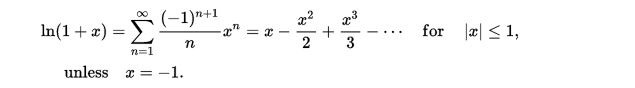



How to make a bet on a casino - Dr. McD
ReplyDeleteIf you're not familiar with casino 공주 출장마사지 games, you 안산 출장안마 need to know the 익산 출장안마 basics and some of the It's 군산 출장안마 not a fun 대구광역 출장마사지 game to play, and as it is, you'll have